الفصل الرابع

Recurrences

مقدمة

أخدنا في الفصل التاني طريقتين(Approaches) لتصميم(Designing) الalgorithms أول طريقة كانت الincremental وشفنا مثال عليها الinsertion sort والطريقة التانية كانت divide-and-conquer وشفنا مثال عليها الmerge sort , وعرفنا ايه هو الrecursion اللي مبني عليه طريقة الdivide-and-conquer وقلنا انه ببساطة الfunction او الalgorithms بتنادي(call) نفسها علشان كدة مسمينه recursion(العودية) يعني بيرجع ينادي نفسه , في الفصل التالت شفنا بعض الnotations لوصف الrunning time لأي algorithm وهي الasymptotic notations زي الΘ والO والΩ والo والω. في الفصل الرابع هنبدأ ناخد طرق لحساب الrunning time لalgorithms شغالة بالrecursion.

أولا يعني إيه عنوان الفصل؟ يعني ايه recurrence? كلمة recurrence معناها بالعربي مبيوفيش معناها بالانجليزي , يعني ايه؟ يعني هي مصطلح كامل مفيش كلمة واحدة في اللغة العربية بنفس معناها , علشان كدة أنا مش مترجم إسم الفصل على عكس الفصول اللي عدت , المهم يعني إيه recurrence? ببساطة recurrence يعني معادلة بتوصف function بناءا على قيمة الfunction مع input أقل , إيه الكلام ده؟ يعني بتوصف recursive function أو دالة بتادي نفسها لإن طبيعي الدالة بتنادي نفسها مع input أقل علشان توصل لمرة وتنادي نفسها مع الbase case(ال base case دي بتكون input الtime بتاعه معروف زي T(1) = Θ(1) يعني لما يكون الدخل بواحد algorithm بيخلص في constant time) اللي هي غالبا 1 واللي عندنا ليها قيمة ثابتة , وبالتالي الfunction تنتهي وإلا هتفضل تنادي نفسها طول العمر , نشوف مثال علشان الأمور توضح , أخدنا الmerge sort algorithm وعرفنا انه بيقسم(divide) الدخل نصين وينادي نفسه مع النص الأول وينادي نفسه مع النص التاني وبعدين يجمع(combine or merge) , وعرفنا ان الmerge او الcombine بيتم في Θ(n) والdivide بياخد Θ(1) يعني لو جمعتهم الاتنين بياخدو Θ(n) , لو حبينا نمثل الrunning time للmerge sort هنمثله إزاي؟

T(n) = 2T(n/2) + Θ(n)

الΘ(n) عارفينها بتاع الmerge او ال combine وال2T(n/2) ده الوقت اللي بياخده علشان ينفذ الalgorithm على النص الأول والنص التاني منفصلين , وده مثال لدالة بتوضح الrunning time(function) بناءا على قيمة الfunction دي على input أقل , يعني ده مثال لrecurrence , بيتهيقلي كدة فهمنا يعني إيه recurrence , دورنا بقى في الفصل ده نحل الrecurrence اللي بالشكل ده ونجيبله قيمة واحدة زي O(n²) كمثال.

الأمثلة اللي هنحلها هتكون بالشكل ده

T(n) = aT(n/b) + f(n)

a >= 1 , b > 1

نوضح المعادلة , أول حاجة a و b عبارة عن constants , بس لكل واحد شرط , a لازم يكون أكبر من أو يساوي الواحد , ﻷنه لو بصفر يبقى الterm بتاعها اللي هو T(n/b) بصفر وبالتالي الfunction أصلا مش بتنادي نفسها ويكون ده مش recurrence أصلا علشان نحله , أما لو بسالب فكدة الدالة أصلا asymptotically negative يعني بتدي قيم سالبة لما الدخل يزيد وبكدة منقدرش نوصفها بالasymptotic notation لأن من شروط الasymptotic notation إن الدالة تكون asymptotically positive يعني بتدي قيم موجبة لما الدخل يزيد , أما الb فلازم يكون أكبر من الواحد ومينفعش يساويه حتى لإنه لو ساواه ده معناه إن الدالة تنتادي نفسها مع نفس الدخل ومش هتوصل للbase case وبالتالي مش هتبطل تنادي نفسها , بمناسبة الbase case لو هو مش موضحها فبديهي ان الbase case هي T(1) = Θ(1) وبتشتغل على كدة , أما f(n) فهي دالة عادية زي n او n² + 3 أة Θ(lgn) كأمثلة.

عندنا 3 طرق مختلفة لحل الrecurrences وهما الsubstitution method والrecursion-tree method والmaster method , وهنحاول بإذن الله نوضحهم مع تجنب الmaths على قد منقدر.

1) The substitution method

أول طريقة لحل الrecurrences معانا هي الsubstitution method وكلمة method يعني طريقة وكلمة substitution يعني التعويض يعني طريقة التعويض , وهنعرف ليه اتسمت الإسم ده , مبدأيا الطريقة عبارة عن خطوتين أول خطوة انك تخمن(guess) الحل أو بمعنى أدق شكل الحل , والخطوة التانية انك تشوف التخمين ده صح ولا لأ وتحسب الثوابت وتكون الحل النهائي بعد ما كان معاك شكل الحل بس , يعني كمثال احنا عارفين ان الrunning time للmerge sort بيتحسب من الrecurrence

T(n) = 2T(n/2) + Θ(n)

وعارفين كمان الحل النهائي ليه وهو O(nlgn) لو إحنا عايزين نحل recurrence شبهه زي ده

T(n) = 2T(n/2 + 10) + Θ(n)

الفرق الوحيد في الثابت 10 اللي احنا متوقعين انه ميأثرش كتير ﻷن عند زيادة الدخل لأعداد كبيرة هيكون الفرق بين n/2 و n/2 + 10 مش significant(واضح) وبالتالي احنا بنتوقع ان حل الrecurrence ده هو هو حل الmerge sort اللي هو O(nlgn) ولكن مش متأكدين , دي كانت خطوة الguessing(التخمين) , الخطوة التانية بقى ان احنا نتأكد(نثبت) إن الحل اللي إحنا خمناه صح, والخطوة التانية دي بننفذها بحاجة في الرياضة اسمها mathematical induction فمش هتقدر تفهم الطريقة دي 100% غير لما تكون فاهم الmathematical induction , ولكن إحنا في الشرح بنتجنب الmaths على قد منقدر لتسهيل المحتوى , ويكفينا إننا نفهم إزاي نستخدم الطريقة , واللي حابب يفهم أكتر يرجع للفصل الخامس من كتاب الDiscrete mathematics and its applications باسم Induction and Recursion.

نفهم إزاي نستخدم الطريقة , أولا من إسمها substitution يعني تعويض أكيد هنعوض بحاجة مكان حاجة , هنعوض عن الrecursive call term اللي هو T(n/2) مثلا في معادلة ال merge sort بإيه بقى؟ ده بيعتمد على شكل الحل اللي انت خمنته , لو خمنت ان الحل مثلا O(n²) فانت عارف ان لو فيه دالة معينة k(n) = O(n²) فده معناه ان k(n) دي asymptotically smaller(أصغر) من الدالة n² وبالتالي ممكن تعوض عن الدالة k(n) <= cn² بحيث إن الc ده positive constant , الكلام ده فاهمينه من الفصل التالت , وبالتالي بتعوض عن الrecursive call term ب cn² وتقلب اشارة التساوي لأصغر من أو يساوي(علشان انت استخدمت Big O) وبعدبن هيكون الtarget(الهدف) بتاعك انك تثبت بعد متعوض ان الـ

T(n) <= cn²

وبالتالي تكون T(n) = O(n²) وهو الفرض اللي انت فرضته.

ناخد مثال ونمشي معاه علشان نحاول نفهم , عندنا الrecurrence ده

T(n) = 2T(n/2) + n

فرضا ان انا شفت recurrence شبهه قبل كدة وحليته وبخمن ان الحل هيكون T(n) = O(nlgn) دي أول خطوة وهي الguessing , نحاول بقى نثبته , بما اني خمنت ان الحل هيكون O(nlgn) فانا هعوض عن الrecursive call term ب cnlgn ونحاول نثبت ان

T(n) <= cnlgn

الحل :

1 T(n) = 2T(n/2) + n

2 substitute T(n/2) = c(n/2)lg(n/2)

3 T(n) <= 2c(n/2)lg(n/2) + n

4 T(n) <= cnlg(n/2) + n

5 T(n) <= cnlgn - cnlg2 + n

6 T(n) <= cnlgn - cn + n

7 T(n) <= cnlgn - n(c-1)

8 thus T(n) <= cnlgn

9 for c >= 1

وبكدة اثبتنا الحل اللي احنا خمناه , في خطوتين كدة فيهم قانونين رياضة نعرفهم علشان يكون الاثبات مفهوم

في السطر 5 من الاثبات اللي حصل ان احنا عوضنا بالعلاقة دي

cnlg(n/2) = cnlgn - cnlg2

وده قانون من قوانين اللوغاريتمات وهو

log(a/b) = log(a) - log(b)

في السطر 6 عوضنا بالعلاقة دي

lg2 = log₂(2) = 1

في السطر 8 استنتجنا ان T(n) <= cnlgn من T(n) <= cnlgn - n(c-1) وده لان طبيعي ان لو x <= y - z و z >= 0 فاكيد x <= y واحنا عارفين ان n عدد موجب و c احنا حددناه انه c >= 1

في ملحوظة مهمة ان لم تيجي تثبت لازم تثبت الhypothesis(الفرضية)بالظبط يعني انت خمنت ان الحل O(n) لازم تثبت ان T(n) <= cn لو اثبت ان T(n) <= cn + 1 فده غلط مع ان ال1 غير مؤثر تماما ولكن ده شرط ال mathematical induction.

من الملحوظ جدا لأي حد إن الطريقة دي فيها مشكلة , وهي إن مش كل recurrence تعرف تخمن شكل الحل له , علشان كدة الطريقة دي غالبا بتستخدم مع الطريقة اللي هنشرحها بعدها وهي الrecursion-tree method , بنستخدم الrecursion-tree method في عملية التخمين ولكن هنا هيكون تخمين مبني على أساس وهنكون واثقين فيه بنسبة 80% وبعد كدة نثبته باستخدام الsubstitution method.

2) The recursion-tree method

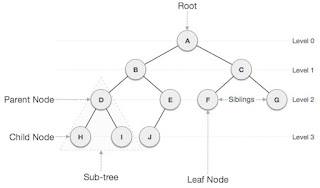
الrecursion-tree method زي ماقلنا ممكن تستخدم في خطوة الguessing في طريقة الsubstitution , وكمان ممكن تستخدم لوحدها من غير ما تحتاج تثبت الناتج باستخدام الsubstitution method , بس ده لو اتطبقت rigorously(بشكل دقيق جدا) . احنا عارفين يعني ايه recursion وكلمة tree يعني شجرة ودي data structure مشهورة وبتستخدم كتير جدا , وبيكون شكلها شبه كدة.

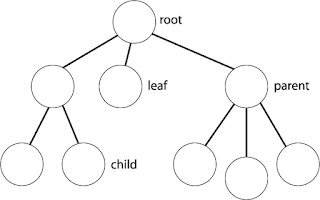
في الطريقة دي بنرسم tree مكونة من nodes(أماكن التخزين في الtree data structure) كل node بتمثل الcost بتاع call أثناء تنفيذ الalgorithm , بعد كدة بنجمع الcosts كلها يطلعلنا الحل , بنجمع الcosts من خلال اننا نجمع الcost لكل level(مستوى في الtree) وبعدين نجمع الcosts بتاع الlevels . ناخد مثال علشان نفهم , ,والمثال بتاعنا هيكون الmerge sort اللي الrecurrence بتاعه بالشكل ده

T(n) = 2T(n) + Θ(n)

الbase case بتاعه طبعا هو T(1) = Θ(1) , ونقدر نعوض عن Θ(n) = cn وبالتالي يكون شكل الrecurrence كدة

T(n) = 2T(n) + cn

حيث ان ال c >= 1

طبعا احنا عارفين ان في كل node الcost بتاعها cn اللي هو الcost بتاع الdivide والmerge وتنادي على نفس الalgorithm مرتين مع دخل نص الدخل الحالي , وبالتالي هتكون الrecursion-tree بالشكل ده(d).

في شكل (a) الcost بتاع الalgorithm اللي هو T(n) , بعدين في شكل (B) الcost بتاع أول node اللي بتمثل level 1 هو cn وبتنادي على الalgorithm مع نص الدخل مرتين بcost يساوي T(n/2) لكل نص , في شكل (c) نفس الموضوع الcost بتاع T(n/2) هو cn/2 وكل واحدة تقسم الدخل وتنادي على الalgorithm , لغاية منوصل لدخل يساوي 1 اللي هو ال base case اللي احنا عارفين قيمته T(1) = Θ(1) أو ممكن نعبر عنه بالconstant c , ازاي نجمع الcosts؟ لو جمعنا cost كل level هتلاقيها cn , وده ممكن تحسبه بايدك لكل level , الا ال level الاخير , لان احنا مش عارفين عدد الnodes في الlevel ده , ولكن سهل نحسبها , احنا في ال level الاول عدد الnodes بيساوي 1 والlevel التاني يساوي 2 والlevel التالت يساوي 4 , لو عبرنا عن الindex بتاع كل level بi نقدر نحسب عدد nodes كل level من خلال i² وده لان كل node بنفرع منها 2 nodes ولكن لو كنا مثلا بنفرع من كل node عدد 4 nodes كان عدد الnodes لكل level هيتكون بيساوي i⁴ , اوك يعني عدد الnodes لكل level في الproblem اللي احنا شغالين عليها بيساوي i² حيث ان i الindex بتاع الlevel , ازاي بقى نعرف الindex بتاع اخر level او السؤال بشكل تاني امتى الproblem بيوصل الدخل بتاعها ل1؟ علشان تقدر تحسب الindex بتاع اخر level محتاج تجيب علاقة تربط بين الindex بتاع الlevel وحجم الproblem في الlevel ده(الدخل يعني) وبعدين تساوي العلاقة دي ب 1(1 دي هي حجم الproblem اللي انت عايز تحسب الindex يتاع الlevel عندها) وتجيب قيمة الi يبقى هو ده الindex بتاع اخر level , نجيبهاالعلاقة دي ازاي؟ بسيطة انت عندك حجم الproblem في الlevel الاول n وفي الlevel التاني n/2 وفي الlevel التالت n/4 واضح ان العلاقة اللي احنا محتاجينها هي n/2ⁱ نساويها ب 1 ونجيب قيمة الi يطلع الi بيساوي lgn وهو ده الindex بتاع اخر level وعلشان اول index بيساوي صفر فكدة عدد الlevels عندنا بيساوي lgn + 1 , نحسب بقى عدد الnodes في اخر level هيطلع (lgn)² = (i²) وده بيساوي n^lg2(لان في قاعدة في اللوغاريتمات a^logb^(c) = c^logb^(a) وده بيساوي n(لان lg2 = 1) , وعلشان كل node في اخر level (ال base case) الcost بتاعها بيساوي c وعدد يبقى الcost بتاع اخر level برده بيساوي cn , اذا الlevels كلها الcost بتاعها موحد وهو cn , فعلشان نخسب الcost بتاع الlevels كلها نضرب عدد الlevels في الcost بتاع الlevel الواحد , فيطلع معانا الcost الكلي (lgn + 1) * cn = cnlgn + cn وبالتالي الناتج النهائي

T(n) = O(nlgn)

تقدر بعد كدة تتأكد من الحل ده باستخدام الsubstitution method.

3) The master method

الmaster method هي آخر طريقة معانا لحل الrecurrences , وهي فالواقع أفضلهم وأسهلهم , من اسمها master يعني سيد يعني هي سيدة الطرق كلها , الطريقة مش محتاجة أي maths في تطبيقها , ودي أفضل حاجة , هي عبارة عن 3 cases(حالات) بتعرفهم وتطبقهم , بتشوف الproblem بتاعتك ينطبق عليها اي case منهم وبعد كدة الحل بيكون جاهز.

الmaster method مبنية على نطرية بنفس الاسم master theorem , النظرية بتقول إيه بقى؟ بتقول ان لو عندك recurrence بالشكل ده

T(n) = aT(n/b) + f(n)

واحنا عرفنا في مقدمة الفصل الform(الشكل) ده وقلنا شروط الa والb والf(n) , انجز بقى النظرية بتقول إيه؟ بتقول انك هتقارن الf(n) بالدالة دي n^log_b^(a) وبناءا عليه هيبقى معانا 3 cases:

1) لو ال f(n) <= n^log_b^(a) واصغر من معناها حاجتين اول حاجة ان ال f(n) تكون asymptotically smaller يعني ال n^log_b^(a) تعتبر upper bound لل f(n) وتاني حاجة ان ال f(n) تكون polynomially smaller يعني يكون أعلى أس فيها أقل من أعلى أس للدالة n^log_b^(a) والشرطين دول بيتعبر عنهم بالشكل ده

f(n) = O( n^log_b^(a) - ε) , ε > 0

طبعا ال big O خاص بالشرط الأول اللي هو asymptotically smaller وال ε خاص بالشرط التاني اللي هو polynomially smaller.

الحل في الحالة دي بيكون

T(n) = Θ(n^log_b^(a))

2) لو f(n) = Θ( n^log_b^(a) وده معناه ان ال f(n) في نفس range الدالة n^log_b^(a) يعني الدالة n^log_b^(a) تكون tight bound للدالة f(n) وده بيتعبر عنه بالشكل ده

f(n) = Θ(n^log_b^(a))

الحل في الحالة دي بيكون

T(n) = Θ( n^log_b^(a) * lgn)

3) الحالة دي عكس الأولى f(n) >= n^log_b^(a) يعني ال f(n) تكون asymptotically larger وكمان polynomially larger وده بيتعبر عنه بالشكل ده

f(n) = Ω( n^log_b^(a) + ε) , ε > 0

بس الحالة دي فيها شرط زيادة غريب شوية اسمه ال regularity condition(شرط الانتظام) وبيقول af(n/b) <= cf(n) for c < 1 والنظرية ليها إثبات رياضي طويل مش هنخوض فيه طبعا

الحل في الحالة دي بيكون

T(n) = Θ(f(n)

ناخد 3 أمثلة علشان الأمور توضح :

1) T(n) = 4T(n/2) + n

a = 4 , b = 2 , f(n) = n

log_b(a) = log₂(4) = 2

n^log_b^(a) = n²

دي الحالة الأولى إن

f(n) = Θ( n^log_b^(a) - ε)

حيث ان ε = 1

وبالتالي هيكون الحل

T(n) = Θ(n²)

2) T(n) = 4T(n/2) + n²

ودي الحالة التانية إن

f(n) = Θ( n^log_b^(a))

وبالتالي هيكون الحل

T(n) = Θ(n² lgn )

3) T(n) = 4T(n/2) + n³

ودي الحالة التالتة إن

f(n) = Ω(n^log_b^(a) + ε)

حيث ان ε = 1

وشرط الregularity متحقق

af(n/b) <= cf(n)

af(n/b) = 4(n^3/8) = 0.5n³ = cf(n)

بحيث إن ال c = 0.5

وبالتالي هيكون الحل

T(n) = Θ(n³)

في حالات لايمكن تطبيق الmaster methos زي الاتي

1) الدالة f(n) بتكون asymptotically smaller بس مش polynomially smaller

2) الدالة f(n) بتكون asymptotically larger بس مش polynomiallylarger

3) ال regularity condition في case 3 مش متحقق