الفصل السادس

Heapsort

مقدمة

اتعرضنا في الباب الأول لل insertion sort algorithm وقلنا ان أهم ميزة فيه هي الـ storage لانه sort in place يعني بيرتب في نفس الـ array مش بيحتاج يحجز memory زيادة ولكن مشكلته ان الـ running time بتاعه O(n²) , واتعرضنا لل merge sort algorithm وقلنا ان أهم ميزة فيه هي الـ speed لان الـ running time بتاعه O(nlgn) ولكن مشكلته انه مش sort in place لانه بيحتاج يحجز memory زيادة عن الـ array اللي بيرتبها(الـ algorithm بيكون sort in place لو بيحجز في الـ memory عدد أماكن زيادة عن الـ data structure بتاعته متزدش عن انها constant لكن لو بيحجز عدد متناسب مع الدخل يعني n أو n/2 أو lgn فده ميعتبرش sort in place) , في الفصل ده هنتعرض لل heapsort algorithm وده algorithm بيجمع الميزة اللي في الـ insertion sort بانه sort in place والميزة اللي في الـ merge sort بان الـ running time بتاعه O(nlgn) .

الـ heapsort بيقدم design approach جديدة غير الـ incremental بتاعة الـ insertion sort وغير الـ divide-and-conquer بتاعة الـ merge sort , الـ design approach الجديدة هي "The use of a data structure" , في الـ design approach دي الـ algorithm بيعتمد اعتماد كلي على data strucure بمعنى ان الـ data structure بترتب البيانات بشكل يناسب الـ algorithm , فلو بنيت الـ data structure صح الـ algorithm بيكون سهل جدا , وال data structure في حالة الـ heapsort هي الـ Heap.

Heaps

كلمة heap ليها استخدامين في علم الكمبيوتر , أول استخدام ك data structure لل heapsort وبعض التطبيقات التانية زي الـ priority queue (ودي هنشوفها في نهاية الفصل) , والاستخدام ده هو اللي هيستمر معانا في باقي الكتاب , وتاني استخدام ك garbage-collected storage يعني مكان فيه garbage data (بيانات أصبحنا مش محتاجينها garbage) زي في الـ memory الـ data اللي استخدمناها وبقينا خلاص مش محتاجينها , وبالرغم من إن الكاتب بيقول إن كلمة heap استخدمت لأول مرة ك data structure مش garbage-collected storage إلا إن معنى كلمة heap أقرب للاستخدام ك garbage-collected storage وده لإن كلمة heap معناها "كومة"(أو شوية حاجات مرميين فوق بعض بدون ترتيب) زي كومة ملابس لسة مترتبوش مثلا , أما ك data structure ومنظمة جدا زي مهنشوف فالمعنى ده مش راكب خالص ودورت فأكتر من قاموس مش لاقي معنى غير كومة , ما علينا أيه هي الـ Heap data structure?

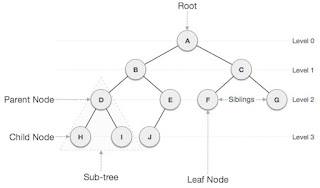
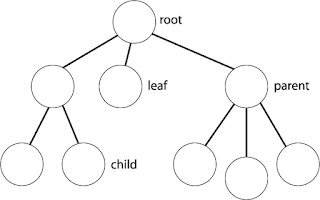
الـ Heap عبارة عن binary tree متخزنة في array , يعني إيه الكلام ده؟ يعني الـ Heap هي array كل عنصر فيها عبارة عن node في binary tree , في الأول احنا عارفين يعني إيه tree وشفناها في الباب الأول , نتأكد ان فيه كام نقطة عارفينها قبل منكمل:

• الـ binary tree يعني كل node ليها حد أقصى 2 children
• الـ node اللي ملهاش parent اسمها root node ودي بتبقى node واحدة في الـ tree
• الـ node اللي ليها child أو اتنين اسمها node ولكن ال node اللي ملهاش children بنسميها leaf
• الرابط اللي بيربط اي parent مع child اسمه edge
• لو اخدت جزء من الـ tree بنسميه subtree
• الـ height بتاع الـ tree هو عدد الـ edges في أطول مسار ل leaf أو عدد الـ levels - 1

والكلام ده موضح في الصورة دي

فيه شرطين لل shape(الشكل) علشان الـ binary tree تبقى heap :

• انك متبدأش تضيف nodes في level جديد إلا لما يكون ال level اللي قبله مكتمل
• انك بتبدأ تضيف من الشمال ل اليمين.

وبناءا على الشرطين دول كل الـ trees دي متنفعش تكون heap

إزاي بنخزن الـ binary tree في array? بنبدأ نخزت الـ nodes من level 0 وننزل لتحت ومن الشمال ل اليمين , مثال:

في الصورة اللي قدامك الـ binary tree اللي في الشكل a هي الـ heap اللي في الشكل b , لاحظ ان الـ nodes متخزنة في الـ array بالترتيب من فوق ل تخت من الشمال ل اليمين , الرقم اللي فوق كل node هو الـ index اللي متخزنة فيه الـ node في الـ array , وزي ماقلنا ان في الكتاب بيعتبر أول index في الـ array هو 1 عكس لغات برمجة كتير , بالتالي الـ root node دايما الـ index بتاعها هو 1 . عايزين نجيب علاقات تحسب لأي node الـ indices بتاعة الـ parent وال left child وال right child لإن هنستخدمهم كتير في الـ algorithm:

• بالنسبة لل parent لو لاحظت هتلاقي انك لو قسمت الـ index بتاع أي node على 2 واخدت الـ floor (يعني لو طلع رقم عشري تاخد الرقم الأقل , كمثال 3 / 1 = 1.5 فال floor هنا ⌊⌋ بيساوي 1 على عكس الـ ceiling ⌈⌉ بيساوي 2 بتاخد الرقم الأكبر) هتجيب الـ index بتاع الـ parent

PARENT(i) = ⌊i / 2⌋

• أما لو عاوز الـ left child فواضح انك لو ضربت الـ index في 2 هيديك الـ index بتاع الـ left ول ضربت وزودت 1 هيديك الـ index بتاع الـ right.

LEFT(i) = i * 2

RIGHT(i) = i * 2 + 1

فيه نوعين من الـ Heap لكل نوع property(خاصية):

1. أول نوع max-heap ود الـ property بتاعته ان أي parent لازم يكون القيمة اللي فيه أكبر من أو تساوي القيم اللي في الـ children بتوعه , يعني لو الـ array اسمها A :

A[PARENT(i)] >= A[i]

وبالتالي أكبر قيمة في الـ tree القيمة اللي في الـ root node اللي هي A[1]

الـ Heap اللي كانت في الصورة اللي فاتت كانت max-heap

2. تاني نوع min-heap وده عكس الـ max يعني

A[PARENT(i)] <= A[i]

وبالتالي القيمة اللي في الـ root node اللي هي A[1] هي أصغر قيمة في الـ tree

في الفصل ده هنستخدم ون implement الـ max-heap وفي الـ implementation الفرق بين الـ max-heap وال min-heap بيكون بسيط جدا.

أي heap عبارة عن array ليها 2 attributes :

• الـ length : عدد العناصر اللي في الـ array
• الـ heap_size : عدد العناصر من الـ array اللي موجودة في الـ heap , وده لإن في الـ running time بنحتاج نحزف عناصر من الـ heap زي مهنشوف في الـ heapsort وبالتالي

heap_size[A] <= length[A]

Building a heap

عملية ترتيب مجموعة أرقام باستخدام الـ heapsort بتتم على خطوتين:

1. أول خطوة هي بناء الـ Heap
2. تطبيق الـ algorithm

ناخد أول خطوة وهي Building the heap , أول حاجة لو عندنا tree عبارة عن node أو parent وليها 2 children أو leaves لو الـ parent أكبر من الـ 2 children فدي max-heap أما لو واحد على الأقل من الـ children أكبر من الـ parent فدي مش max-heap وعلشان نخليها max-heap نبدل الـ parent مع أكبر child فيها , لو طبقنا العملية البسيطة دي من تحت لفوق على الـ tree كلها هنوصل في الاخر ل max-heap كاملة. ببساطة ال tree عبارة عن قسمين , قسم ال nodes(اللي ليها children) وقسم ال leaves (اللي ملهاش children) , الـ leaves موجودة في اخر الـ tree من تحت , لو مسكنا أول nodes من تحت اللي فوق الـ leaves مباشرة , وطبقنا عليها العملية البسيطة اللي شرحناها وطلعنا على الـ parents بتاع الـ nodes دي وطبقنا نفس الـعملية وهكذا هنوصل ل max-heap , بالطريقة دي هنحتاج 2 procedure , واحد ي maintain (يعدل) الـ max-heap proerty زي ما وصفنا وده هنسميه max_heapify والتاني ينادي على الـ max_heapify مع كل الـ nodes من تحت لفوق لغاية مال array كلها تتحول ل heap.

ازاي نفرق بين الـ nodes والـ leaves علشان نطبق الـ max_heapify على الـ nodes من تحت لفوق؟ من خصائص الـ heap قدرنا نثبت إن لأي heap عدد عناصرها n هيكون من 1 ل ⌊n / 2⌋ هما الـ nodes و من 1 + ⌊n / 2⌋ ل n هما الـ leaves وبالتالي المفروض ان احنا نطبق الـ max_heapify على العناصر من ⌊n / 2⌋ ل 1 (من تحت لفوق).

الـ max_heapify بياخد دخل عبارة عن الـ array وال index بتاع الـ node اللي هيطبق عليها , بديهيا ان الـ node اللي هتجيلنا في الـ max_heapify الـ right وال left بتوعها هما max-heap لإن احنا بنطبق الـ procedure من تحت لفوق وأول nodes من تحت ملهاش غير 2 leaves وبالتالي الـ leaves دي تعتبر max-heap لان ملهاش children أكبر منها , فيه مشكلة واحدة ان الـ max_heapify ممكن في وسط الـ tree يبدل parent مع child (ﻷنه لقي الـ child أكبر) فال parent ده يكون أصغر من الـ children الجداد بتوعه فلازم تضطر تنادي على نفس الـ procedure مع أي node تبدلها وال procedure يكون يقدر ي terminate لو الـ sub-tree تمام من ناحية الـ max-heap property.

دلوقتي نقدر نشوف الـ pseudocode بتاع الـ max_heapify .

1. سطر 1 و 2 بيحسب الـ indices بتاعة الـ right وال left لل node
2. سطر 3 و 4 و 5 بي check ان الـ left index بيمثل عنصر من عناصر الـ heap يعني مش اكبر من الـ heap_size وبعدين لو العنصر ده أكبر من الـ node اللي هي الـ parent بتاعته بيحفظ ال index بتاعها في متغير اسمه largest لو مش اكبر يبقى الـ largest هو الـ index بتاع الـ node
3. سطر 6 و 7 بيعمل نفس الحوار مع الـ right بس لو هو مش اكبر من الـ parent بتاعه مش هيعمل حاجة لانه مخزن ان الـ index بتاع الـ parent هو الاكبر وبالتالي مفيش حاجة اتغيرت
4. سطر 8 و 9 و 10 بي check لو الـ largest مش الـ index بتاع الـ node يعني اتغيرت لل left أو الـ right فبالتالي اللي اتغيرله ده أكبر من الـ parent بتاعه فهيعمل swap او exchange وينادي على نفس الـ procedure مع الindex الجديد ده أما لو الـ largest هو هو الـ index بتاع الـ node اللي اتبعتت لل procedure فكدة مفيش حاجة تتغير و terminate

 

الصورة دي بتوضح تنفيذ الـ max_heapify على node في tree

نحسب الـ running time لل max_heapify procedure? ممكن نحسب الـ running time باستخدام الـ recurrence ونحل الـ recurrence باستخدام الـ master method ولكن الموضوع هنا أبسط, الخطوات من سطر 1 ل 9 بتتنفذ في constant time يعني O(1) وبما ان ال worst-case هي ان الnode تتحرك من أعلى ال tree اللي هي ال root لأسفل ال tree , في كل مرة تنفذ نفس الخطوات اللي ال running time بتاعها constant , فال running time الكلي هو O(lgn) لان ال height بتاع ال tree هو O(lgn)

نشوف الـ pseudocode بتاع الـ procedure اللي هيبني الـ heap وهو الـ build_max_heap من خلال انه ينادي على الـ max_heapify procedure , الـ procedure بياخد كدخل الـ array اللي هتتحول ل heap

 

1. سطر 1 بيعمل initialization لل heap_size , في البداية الـ heap_size هو هو الـ length بتاع الـ array
2. سطر 2 و 3 بي loop على الـ nodes وينادي الـ max_heapify مع كل node (لاحظ انه بيعدي على العناصر من ⌊n / 2⌋ ل 1 اللي هما الـ nodes والباقي leaves)
   
   
   والصورة دي بتوضح تنفيذ الـ build_max_heap على array

نحسب الـ running time لل build_max_heap? ال build_max_heap ما الا بينادي على ال max_heapify عدد O(n) times فبالتالي ال running time الكلي هيكون O(nlgn) , ولكن لان ال max_heapify بيتنادى على نص ال n وكمان ال max_heapify مرات كتير بياخد consant time فال running time اللي حسبناه ده مش asymptotically tight (واحنا عارفين يعني ايه asymptotically tight من الباب الاول) فبحسبة رياضية علشان يوصل لل asymptotically tight وصل لان ال running time هيكون linear يعني O(n).

Implementation note

لو انت مدرستش assembly ممكن تعدي الـ note دي , لو لاحظت في الـ build_max_heap اكتر حاجة بنفذها اننا بنادي على الـ max_heapify , واكتر حاجة بنفذها في الـ max_heapify هي دوال الـ left وال right , فلو سرعنا تنفيذ الدالتين دول هنحسن اداء الـ algorithm بشكل كبير , دالة الـ left بتضرب الـ index في 2 وده ممكن يتعمل في الـ assembly بخطوة واحدة وهي shift left ودالة الـ right بتضرب في 2 وتجمع 1 وده ممكن يتعمل على خطوتين shift left وبعد كدة تزود على مستوى الـ binary ب 1 , المشكلة بقى ان احنا لما نعملهم ك functions عادية بيخزن الـ instructions بتاع الـ function في مكان ما ك procedure وكل متنادي الـ function دي يعمل jump لمكان الـ procedure ولما يخلص يعمل return للمكان اللي عمل منه jump , يعني خطوتين او اكتر في عملية الـ jump وال return وهو اصلا الـ procedure عبارة عن خطوة او 2 , لو الـ procedure ده عبارة عن 100 instructions مثلا كانت خطوة الـ jump وال return بالنسباله متاثرش ولكن بما ان الـ jump وال return بتاخد cost يساوي الـ procedure نفسه فمن الافضل اننا نتخلص منه , في الـ c في حاجة اسمها macro وحاجة اسمها inline function بتعمل الحوار ده , بدل متخزن الـ procedure في مكان وكل متنادي عليه يعمل jump و return بيعمل حاجة بديلة , بيكرر الـ instructions في كل مكان بتنادي فيه على الـ procedure وبكدة بيوفر الـ cost بتاع الـ jump وال return , لو عاوز تعرف inline function بتحط قبل التعريف الطبيعي الـ keyword دي "inline" أما لو عاوز تعرف macro بتعرفه بالشكل ده كمثال

#define left(i) i*2

لو عاوز تعرف الفرق بين الـ macro وال inline function ممكن ترجع للينك في الـ references عن الموضوع , وفي الـ implementation لل heapsort اللي هسيب اللينك بتاعه هتلاقيني مستخدم الـ macro.

The heapsort algorithm

دلوقتي نقدر ننفذ الـ heapsort algorithm بكل سهولة , الـ procedure اللي هينفذ الـ heapsort اسمه heapsort وبياخد دخل الـ array اللي هيتعملها sorting , الـ algorithm بسيط جدا , أول خطوة نبني الـ heap باستخدام الـ build_max_heap procedure , بعد كدة هيكون معانا أكبر عنصر في الـ array موجود في الـ root node يعني A[1] , العنصر ده أكبر واحد فبالتالي مكانه الصحيح في اخر ال array فنعمله swap او exchange مع اخر عنصر في ال array وكدة العنصر الاخير ده عايزين نطلعه من ال heap فننقص ال heap size بواحد , بعد كدة ننادي على ال max_heapify مع ال root node اللي احنا لسة عاملنله swap علشان اكيد عمل violation لل max-heap property , ونكرر العملية دي عدد n-1 من المرات لان اخر عنصر هيكون لوحده في ال heap وبالتالي هيكون اصغر عنصر وموجود في مكانه الصحيح.

وده الـ pseudocode لل heapsort algorithm

1. سطر 1 بيبني الـ heap
2. سطر 2 بي loop على عناصر الـ array ماعدا اخر عنصر
3. سطر 3 بيعمل exchange للroot مع اخر عنصر(اللي هيتغير كل iteration)
4. سطر 4 بيقلل الـ heap_size بواحد علشان لما ينادي على الـ max_heapify مياخدش اخر عنصر (اللي هو خلاص رتبه وحطه في مكانه الصحيح) معاه في الحسبان
5. سطر 5 بينادي على الـ max_heapify مع الـ node علشان ترجع max-heapبعد مال exchange عملها violatin

ودي صورة بتوضح تنفيذ الـ algorithm على array

نحسب الـ running time لل heapsort algorithm؟ أول سطر بياخد O(n) وال for loop بتنادي على الـ max_heapify عدد n - 1 من المرات وال max_heapify بياخد O(lgn) فبالتالي الـ for loop بتاخد O(nlgn) وبالتالي الـ algorithm كله بياخد O(nlgn)

وفي النهاية ده implementation لل heapsort بلغة الـ c

https://github.com/hossamnasser938/Introduction-to-Algorithms-TextBook/blob/master/heap_sort.c

  

Priority Queues

أول تطبيق لل Heap data structure كان الـ Heapsort algorithm , تاني تطبيق هو الـ priority queue , كلمة queue يعني طابور وهي data structure بذاتها وهيتم شرحها باذن الله في الباب التالت , أما كلمة priority فمعناها أولوية , يعني الـ priority queue عبارة عن طابور من مجموعة أشياء مرتبين حسب الأولوية , الأولوية هنا هي الـ key , بتستخدم في إيه الـ priority queue? ليها استخدامات كتير منها على سبيل المثال الـ Job scheduling , وهو إن في الـ processors الحديثة البرنامج بيتقسم لمجموعة من الـ jobs أو الـ tasks ويتنفذوا in parallel (على التوازي أو في نفس الوقت), مين يتنفذ قبل مين ده إسمه الـ job scheduling , وفيه أكتر من approach لل scheduling منها الـ priority scheduling , وفي الـ approach دي الـ tasks بتاخد قيم priorities وبناءا على القيم دي بيحصل scheduling يعني اللي الـ priority بتاعتها أعلى بتتنفذ الأول.

فيه نوعين من الـ priority queue هما max-priority queue و min-priority queue , نفس الحوار اللي في الـ heap , هنا هنعمل implementation لل max-priority queue ولو حبيت تعمل min مش هتغير كتير , أول حاجة طبعا هنستخدم الـ procedures اللي استخدمناها واحنا بنبني الـ heap وهما الـ max_heapify وال build_max_heap , إيه بقى العمليات اللي هحتاج أعملها على الـ heap علشان تخدم الـ priority queue , هما 3 عمليات :

1. extract_max(A)
2. increase _key(A, i, k)
3. insert(A, k) 

في الـ procedure الأول extract_max عايزين نعرف العنصر الأعلى priority في الـ queue , وهنا فيه نوعين: إما عايز أعرف بس وهنا هنسميه heap_maximum(A) وإما عايز أعرفه وأشيله من الـ queue لإني خلاص هنفذ الـ task دس فمش عايزها تفضل في الـ queue وهنا هنسميه heap_extract_max(A). طبعا احنا عارفين ان في الـ max-heap العنصر صاحب أعلى key بيكون في الـ root node أو أول مكان في الـ array , فبالتالي لو عاوز أرجع العنصر صاحب أعلى أولوية ببساطة برجع أول عنصر في الـ array.

طبعا الـ running time بتاع الـ heap_maximum هو O(1)

أما لو عاوز أعمل extraction أو أشيل العنصر صاحب أعلى priority فهنا في مشكلة اني محتاج بعد ما أشيله اظبط الـ heap علشان مدمرش الـ structure بتاعها , ففي الحالة دي ببساطة هبدل الـ root node باخر node وكدة يبقى اخر node هي اللي هرجعها , بعد كدة انادي على الـ max_heapify مع الـ root node الجديدة علشان يظبط الـ heap .

• في سطر 1 و 2 بيتأكد ان الـ heap فيها عناصر علشان يقدر يرجعها ودي أول مرة يعمل error handling في الـ pseudocode لأنه قال في بداية الكتاب انه مش هيضيف الـ error handling لان وظيفة الـ pseudocode انه يبين فكرة الـ algorithm , ما علينا
• سطر 3 بيحفظ الـ root node للي هيرجعها في متغير اسمه max
• سطر 4 بيبدل الـ root node مع اخر node
• سطر 5 بيقلل الـ heap_size والخطوة دي معناها انه حذف اخر عنصر في الـ heap اللي هو هيرجعه
• سطر 6 بينادي على الـ max_heapify مع الـ root node
• سطر 7 بيرجع الـ max

الـ running time بتاع الـ heap_extract_max هيكون O(lgn) لان كل الخطوات بتتنفذ في constant time ماعدا الـ max_heapify بيتنفذ في O(lgn)

 

في الـ procedure التاني increase_key عايزين نزود الـ priority بتاع عنصر معين , الـ procedure هيجيله دخل الـ heap وال index بتاع العنصر اللي هزودله الـ priority وقيمة ال priority الجديدة , المفروض ان انا هعمل assignment لل priority الجديدة في ال عنصر بال index اللي جالي , ولكن بعد ماعمل assignment لازم اتاكد ان الـ max-heap لسة الـ property بتاعتها محصلهاش violation لان ممكن الـ priority الجديد تكون أعلى من الـ parent بتاعها , وبالتالي هضطر اعمل loop كل مرة اقارن الـ priority الجديدة مع الـ priority بتاع الـ parent بتاعها لو الجديدة اكبر اعملهم exchange , ولو وصلت لل root node اخرج من الـ loop.

• سطر 1و 2 بيتاكد ان الـ priority الجديدة فعلا اكبر من القديمة والا عملية الـ increase مش صحيحة
• سطر 3 بيعمل assignment لل priority الجديدة
• سطر 4 و 5 و 6 بيعمل الـ loop زي ما وضحناها

وفي الصورة دي بيوضح عملية الـ increase بالخطوات

الـ running time بتاع الـ heap_increase_key هو O(lgn) لان الخطوات اللي قبل الـ loop بتتنفذ في constant time وال loop في O(lgn) لان طول الـ tree هو O(lgn)

في الـ procedure التالت max_heap_insert عايز يضيف عنصر جديد في الـ heap , فهيعمل trick جامدة , بدل ميفضل يدور هو المفروض يضيف الـ node دي فين في الـ heap , هيضيفها في اخر الـ heap ويديها قيمة سالبة مالا نهاية علشان يتاكد انها اقل من الـ priority بتاعتها وبعدين ينادي على الـ increase procedure ويديه قيمة الـ priority الفعلية وهو يحطها في مكانها الصحيح.

• سطر 1 بيزود الـ heap_size ب 1 علشان يضيف الـ node الجديدة
• سطر 2 بيحط سالب مالانهاية في الـ node الجديدة
• سطر 3 بينادي على الـ heap_increase_key مع الـ node الجديدة ويديها الـ priority اللي جاتله في الدخل

الـ running time بتاع الـ max_heap_insert هو هو الـ running time بتاع الـ heap_increase_key وهو O(lgn)

وفي النهاية ده implementation لل max-priority-queue بلغة الـ c

https://github.com/hossamnasser938/Introduction-to-Algorithms-TextBook/blob/master/priority_queue.c

References used other than the textbook

• Macro and inline functions

http://icarus.cs.weber.edu/~dab/cs1410/textbook/6.Functions/inline.html

• Priority queue

http://pages.cs.wisc.edu/~vernon/cs367/notes/11.PRIORITY-Q.html