الفصل الثامن

Sorting in Linear Time 

مقدمة

في الفصول اللي عدت شفنا أكتر من algorithm بيحل مشكلة ال sorting , بداية من ال Insertion sort لل Merge sort لل Heap sort لل Quicksort , ولكن إيه أفضل performance وصلناله من حيث ال running time؟ الإجابة هي إن أفضل running time وصلناله هو O(nlgn) في ال worst case , السؤال بقى هل فيه أفضل من كدة؟ هل نقدر نعمل design ل Sorting algorithm يشتغل في running time أقل من O(nlgn)؟ الإجابة أه نقدر , بس لازم نغير الطريقة اللي بنفكر بيها , طيب هي إيه الطريقة اللي بنفكر بيها ومحتاجين نفكر بطريقة غيرها؟ أو السؤال بشكل تاني إيه المتشابه في كل ال algorithms اللي شفناها لغاية دلوقتي؟ في كل ال algorithms اللي شفناها لغاية دلوقتي أحنا بنحاول نجيب ال sorted order من خلال المقارنة (comparing) بين ال elements أو الأرقام اللي احنا بنرتبها , يعني في كل algorithm بنعمل عملية comparing بين ال elements وبعضها ومن خلال ال comparing بنعرف ال relative order يعني مين أكبر من مين وبالتالي نوصل لل sorted order , في الفصل ده هنشوف إن أي algorithm بيشتغل بطريقة ال comparing لا يمكن يوصل ل running time أقل من O(nlgn) في ال worst case , أو بمعنى تاني أي algorithm شغال بطريقة ال comparing ال running time بتاعه Ω(nlgn) يعني ال nlgn هي lower bound (حد أدنى) لل running time بمعنى إن مفيش أقل من كدة , كمان في الفصل ده هنشوف 3 algorithms بيشتغلو بطرق غير ال comparing وال lower bound بتاع ال comparing لا ينطبق عليهم , وبالتحديد ال 3 algorithms دول بيشتغلوا في linear time يعني O(n) زي معنوان الفصل بيقول Sorting in Linear Time , ال 3 algorithms دول هما ال Counting sort وال Bucket sort وال Radix sort وهنشوف كل algorithm بالتفصيل بإذن الله.

Lower bounds for sorting

في السكشن ده عايزين نثبت إن أي comparison-based sorting algorithm ال running time بتاعه Ω(nlgn) في ال worst case , من خلال الإثبات ده نقدر نتأكد إن ال Merge وال Heap هما theoretically (نظريا) أفضل algorithms بتشتغل بطريقة ال comparing وإن ال Quick sort أفضلهم practically (عمليا) , وبالتالي نقدر نحاول نفكر في طريقة تاني غير ال comparing وإحنا متأكدين إن إحنا جبنا أفضل حاجة في الطريقة دي قبل منفكر في غيرها.

أول خطوة عايزين نعمل mathematical model (نموذج رياضي) يمثل أي comparison sort algorithm , يعني طريقة تمثل الخطوات اللي بيعملها أي comparison sort algorithm علشان يوصل لل sorted order , وبالتالي نقدر نثبت من خلاله ال lower bound اللي احنا عايزين نثبتها , أو إن عدد الخطوات اللي بياخدها أي comparison sort algorithm بتخضع لل lower bound في ال worst case علشان تقدر توصل للحل.

ال mathematical model اللي هنستخدمه هو ال decision-tree model ومن إسمها هي binary tree بتمثل عملية ال comparison بين 2 elements اللي بتمثل ال base (الأساس) أو العملية الأساسية لأي comparison sort algorithm , في ال model ده إحنا بنهمل أي عملية خلاف ال comparison , زي عمليات ال data movement أو ال swap كمثال , وده لإن إحنا بنثبت lower bound , فلو أخدنا في إعتبارنا عمليات ال comparison بس وأثبتنا ال lower bound فلا شك إن ال lower bound صحيحة مع كل عمليات ال algorithm.

في الصورة اللي قدامك decision tree بتمثل ال Insertion sort (كمثال ل comparison sort algorithm) على دخل مكون من (a1, a2, a3) , في ال tree دي:

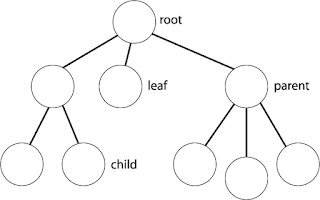
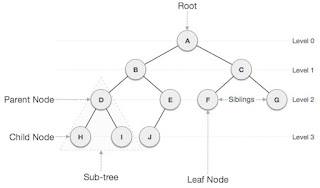
• كل interior node (يعني node ليها children) بتمثل عملية comparison بين 2 elements من الدخل , يعني كمثال ال root node عبارة عن (1:2) وده معناه عملية comparsion بين العنصرين a1, a2.
• كل leaf node (يعني node ملهاش children) عبارة عن خرج لل algorithm , يعني ال algorithm نفذ مجموعة خطوات ووصل لحل معين , يعني كمثال أول leaf node على اليمين عبارة عن (1, 2, 3) وده معناه إن خرج ال algorithm في الحالة دي عبارة عن ال sequence ده (a3 <= a2 <= a1).
• كل transition أو سهم من node في level ل node في level أعلى منه (اعتبارا ان ال level بتاع ال root node هو level 0) بيوضح نتيجة عملية ال comparison اللي تمت , يعني كمثال ال root node بتقارن بين العنصر الأول والتاني فلو الأول أصغر من أو يساوي التاني هنتحرك في ال transition الشمال ولو الأول أكبر من التاني هنتحرك في ال transition اليمين وفي الحالتين هنروح لعملية جديدة , أو بعض ال transitions بتوصلك لناتج لل algorithm لو ال node اللي بتوصلك ليها هي leaf node.

لو ركزنا هنلاقي ان ال tree بتمثل كل الخطوات اللي ممكن ال insertion sort يعملها لو الدخل 3 elements مهما كانت ال elements دي , وحسب ال elements بنوصل ل leaf node بتمثل الحل , كمثال لو الدخل عبارة عن (a1 = 6, a2 = 8, a3 = 5) هتكون الخطوات اللي هياخدها ال algorithm علشان يوصل للحال عبارة عن الخطوات المتحددة بالمسار المظلل في الصورة , يعني في الأول بيقارن الأول(a1 = 6) بالتاني(a2 = 8) فيلاقي الأول أصغر , فيقارن التاني(a2 = 8) بالتالت(a3 = 5) فيلاقي التالت أصغر, فيقارن الأول(a1 = 6) بالتالت(a3 = 5) فيلاقي التالت أصغر فيكون الحل عبارة عن (a3 <= a1 < a2).

إحنا عايزين نعرف إيه أقل عدد من الخطوات(كدالة في الدخل) ممكن يعملها ال algorithm علشان يرتب أي دخل مكون من n elements , ويكون ده ال lower bound اللي احنا عايزين نثبته, إحنا عارفين إن عدد الخطوات للوصول لأي حل هو عدد ال transitions من ال root node لغاية ال node اللي فيها الحل ده (اللي هي leaf node) , وده بالظبط هو ال height بتاع ال tree , لإن ال height هو عدد ال transitions من ال root node لأبعد leaf node , بس إحنا مش عايزين عدد ال transitions لأبعد leaf , إحنا عايزينها ﻷقرب leaf لإن إحنا بنحسب ال lower bound , في الحقيقة الجزئية دي متفرقش لسببين: الأول إن ال decision-tree هي full binary tree , يعني ال leaf nodes بتبقى في ال level الأخير واللي قبل الأخير بس, التاني لإن الفرق ده constant وإحنا بنحل المشكلة asymptotically فبنهمل ال constants , يعني من الاخر إحنا عايزين نحسب ال lower bound لل height بتاع ال tree دي ويكون هو ده ناتج الإثبات بتاعنا. في كام معلومة عايزين نعرفهم:

• علشان ال algorithm يكون correct لازم يكون قادر إنه ينتج ك output أي permutation من الدخل (إحنا عارفين إن permutation يعني إعادة ترتيب للدخل).
• عدد ال permutation لمجموعة عناصر عددها n هو !n (يعني مضروب n).
• ده معناه إن عدد ال leaves لا يمكن يكون أقل من !n , وبالتالي لو رمزنا لعدد ال leaves ب l يبقى n! <= l .
• لو رمزنا لل height ب h , عدد ال leaves في أي binary tree بيساوي على الأقل 2^h , يعني l <= h² .

نقدر نستنتج إن : n! <= l <= h²

وبالتالي : n! <= h²

لو خدنا lg للطرفين : lg(n!) <= h (نقدر ناخد lg للطرفين لان الدالة lg تعتبر monotonically increasing)

وبالتالي : h = Ω(nlgn) (ودي الكاتب أثبتها رياضيا)

Counting sort

 

دلوقتي هنشوف أول algorithm بيشتغل في running time أقل من Ω(nlgn), أو بالتحديد أول algorithm بيشتغل في O(n) أو in linear time , ال Counting sort هو algorithm مبني على فرضية , الفرضية هي إنك لو عرفت لكل عنصر i في ال input عدد العناصر اللي قيمتها أقل من قيمة ال i , فبالتالي تقدر مباشرة تحط i في مكانه الصحيح , يعني كمثال لو عندك input معين فيه العنصر 105 وقدرت تعرف إن ال input ده عدد العناصر اللي قيمتها أقل من 105 هي 50 عنصر فالعنصر 105 المفروض مكانه الصحيح في المكان 51 , ده الأساس اللي مبني عليه ال counting sort , مشكلة ال counting sort إنه عليه بعض ال constraints (القيود), زي:

• لازم عناصر الدخل تكون موجبة.
• لازم عناصر الدخل تكون قيمها في range محدد , يعني كمثال تقدر تحدد مسبقا إن العناصر اللي جاية في ال input قيمها لا تزيد عن 100000.

الشرطين اللي فاتوا لازم يتحققوا علشان ال algorithm يشتغل correctly.

• لازم يكون ال range اللي بتتراوح فيه قيم عناصر الدخل يكون أقل asymptotically من عدد عناصر الدخل, يعني لو رمزنا لعدد عناصر الدخل ب n, ورمزنا لأكبر قيمة لعناصر الدخل ب k (يعني عتاصر الدخل قيمها بتتراوح من 0 ل k) فلازم يكون الشرط ده متحقق :           k = O(n).

الشرط اللي فات لازم يتحقق علشان ال algorithm يشتغل efficiently (يعني in linear time).

نشوف ال pseudocode ل counting sort :

• ال algorithm بياخد دخل عبارة عن: A هي ال input array, و B هي ال output array , و k وهي القيمة اللي بتحدد ال range اللي بتتراوح فيه قيم عناصر الدخل.
• ال algorithm كمان بيحتاج array حجمها k , يستخدمها ك temporary storage (مساحة تخزين مؤقتة), وبالتالي ال algorithm لا يعد sort in place.
• أول حاجة عايزين نحسبها هي لكل عنصر i في ال input array A عدد العناصر اللي قيمتها أصغر من i وعايزين نخزن المعلومات دي في ال array C.
• في السطر 1 : 2 بيعمل initialization لعناصر ال array C بصفر.
• في السطر 3 : 4 بيعدي على عناصر array A , لكل عنصر i في A بيزود بواحد المكان اللي في ال array C واللي ال index بتاعه بيساوي i , وبالتالي كل عنصر في ال array C ال index بتاعه بيعبر عن عنصر في ال array A والقيمة اللي فيه هي عدد مرات تكرار العنصر ده في ال array A, يعني كمثال لو ال array A فيها رقم 10 اتكرر 17 مرة فال array C المكان اللي ال index بتاعه 10 هيكون فيه قيمة 17 وده معناه ان العنصر 10 اتكرر 17 مرة في ال array A.
• في السطر 6 : 7 بيعدي على عناصر ال array C بيخلي قيمة كل عنصر هي مجموع القيمة اللي فيها والقيمة اللي قبليها , وبالتالي كل عنصر في array C ال index بيشاور على عنصر في array A والقيمة بتحدد عدد العناصر اللي أصغر من أو يساوي العنصر في ال array A , كمثال لو أول مكان في array C اللي ال index بتاعها 0 فيه قيمة 2 فده معناه إن العنصر 0 اتكرر مرتين في ال array A, ولو تاني عنصر في array C اللي ال index بتاعه 1 فيه قيمة 4 فده معناه إن العنصر 1 اتكرر 4 مرات في ال array A , فيعد تنفيذ السطرين دول المكان التاني في ال array C هيكون القيمة اللي فيه 6 وده مجموع العناصر اللي بتساوي 1 أو أصغر منه (0).
• تاني حاجة عايزين نحط كل عنصر في مكانه الصحيح.
• في السطر 9 : 11 بيعدي على عناصر ال array A بشكل عكسي يعني بداية من اخر عنصر وانتهاءا بأول عنصر(سطر 9), في كل مرة بيجيب عنصر من array A من خلال A[j] ويجيب المكان اللي المفروض يتحط فيه في ال array B (ال output) من خلال C[A[j]], وبعدين يحط العنصر ده في مكانه الصحيح في array B من خلال B[C[A[j]]] = A[j] (سطر 10), وبعدين يقلل C[A[j]] بواحد (سطر 11).

ليه الخطوة الأخيرة الغريبة دي؟

• أول حاجة ليه بيقلل بواحد في سطر 11؟ علشان هو لكل عنصر في array C ال index بتاعه i مخزن عدد العناصر اللي في array A أقل من أو يساوي i وبالتالي لو فيه عنصر في array A قيمته 10 وفيه 5 عناصر أصغر منه وهو اتكرر 3 مرات فبالتالي المكان اللي ال index بتاعه 10 في array C فيه قيمة 8 ,وأنا عايز أحط ال 3 عناصر اللي قيمتهم بتساوي 10 في الأماكن 6 و 7 و 8 , فأول مرة هحط العنصر في مكان 8 بعد كدة المرة الجاية لما أقابل العنصر 10 وأنا بلف في ال loop لازم ألاقي في array C قيمة 7 علشان أحط العنصر المرة دي في المكان 7 علشان كدة خطوة ال decrement.
• تاني حاجة ليه ب loop بالعكس في سطر 9؟ علشان يحتفظ بترتيب الدخل هو هو في الخرج , يعني لو عنصرين قيمتهم بتساوي x في array A واحد ظهر في array A قبل التاني هنسمي اللي ظهر الأول x1 واللي ظهر التاني x2 , عايز لما نرتب في array B العنصر x1 يظهر قبل x2 (نفس ترتيبهم في array A) , طيب ليه ما هما ليهم نفس القيمة؟ الخاصية دي إسهما stability ودي مفيدة لما تكون بترتب records عبارة عن key data and satellite data (لو مش فاهم إرجع لمقدمة الباب التاني) , وكمان مفيدة لما نستخدم ال counting sort ك subroutine لل radix sort , ال stability of counting sort مهمة جدا لل correctness of radix sort , هنشوف الكلام ده بالتفصيل بإذن الله.

في الشكل اللي قدامك توضيح لخطوات ال counting sort عل الدخل (3, 0, 3, 2, 0, 3, 5, 2):

• في (a) بيوضح array A وخطوة ال construction ل array C اللي هي في سطر 1 : 4 في ال algorithm.
• في (b) بيوضح خظوة تعديل array C اللي في سطر 6 : 7 في ال algorithm.
• في (c) بيوضح تنفيذ أول iteration من ال loop اللي في سطر 9 : 11 من ال algorithm وهي بيحط اخر عنصر(3) من array A(الدخل) في مكانه الصحيح في array B(الخرج).
• في (d) بيعمل تاني iteration مع العنصر القبل الأخير(0).
• في (e) بيعمل تالت iteration مع العنصر القبل القبل الأخير(3).
• في (f) يوضح ناتج ال algorithm.

في النهاية ال running time بتاع ال counting sort هو Θ(n + k) لإن ال algorithm عبارة عن:

• عدد 2 loops عدد ال iterations فيهم k (ال loops سطر 1 و 6).
• عدد 2 loops عدد ال iterations فيهم n (ال loops سطر 3 و 9).

وبما إن k = O(n) فال running time هيكون Θ(n) يعني linear time.

وده implementation لل Counting sort بلغة ال C :

https://github.com/hossamnasser938/Introduction-to-Algorithms-TextBook/blob/master/counting_sort.c

Radix sort

تخيل انك معاك مجموعة dates (تواريخ) كل تاريخ عبارة عن (يوم - شهر - سنة) وعايز ترتبهم , الطريقة البديهية إنك بتبدأ ترتبهم بناءا على السنين , وبعدبن لو فيه elements متشابهة في السنين بترتبهم بناءا على الشهور , ولو اتشابهو كمان في الشهور بترتبهم بناءا على الأيام. يعني كمثال لو معاك ال dates دي:

أول خطوة هترتبهم بناءا على السنين بالشكل ده :

تاني خطوة تمسك الـ elements المشتركة في نفس السنة وترتبهم لوحدهم بناءا على الشهر بالشكل ده :

تالت خطوة تمسك ال elements المشتركين في نفس الشهر ونفس السنة وترتبهم لوحدهم بناءا على اليوم بالشكل ده :

وبكدة نكون رتبنا ال dates .

الطريقة دي ممكن نعملها algorithm مش بس يرتب ال dates ولكن يرتب الأرقام العادية , من خلال إنه يرتبهم في الأول بناءا على ال digit اللي لها أعلى قيمة (ال digit اللي على الشمال وده بتسمى ال most significant bit) زي ال year في مثال ال dates , وبعدين يرتبهم بناءا على ال digits الأقل في القيمة واحدة واحدة لغاية ميوصل لل least significant bit (اللي هي ال digit اللي على الشمال وبتكون قيمتها أقل قيمة) , بالطريقة دي انا بلف عدد من المرات بتساوي عدد ال digits في الأرقام وفي كل مرة بطبق sorting algorithm يرتب الأرقام بتاعتي بناءا على ال digit الحالية بس , فلو استخدمت ال counting sort هستفاد إن ال k هنا قليلة جدا (اللي هي في الحالة دي الأساس بتاع النظام , لو نظام عشري مثلا هيكون ال k بيساوي 9 , لإن أي digit قيمتها مابين 0 و 9) , فهطبق ال counting sort عدد من المرات بيساوي عدد ال digits(اللي هو بيكون constant) , فهنا أنا حليت مشكلة ال counting sort إنه كان لازم ياخد أرقام في range محدد , دلوقتي يقدر ياخد أي أرقام , ومازال ال running time يعتبر linear لإني بطبق ال counting sort عدد constant من المرات (اللي هو عدد ال digits).

مشكلة الطريقة دي إنك محتاج temporary storage كبيرة , لإنك كل مترتب على digit معينة زي ال year في المثال بتاع ال dates محتاج تفصل ال elements اللي ليهم نفس ال year علشان تقارن الشهور بتاعتهم ولو اتساوو بعض ال elements في الشهر محتاج تفصل المشتركين مع بعض علشان تقارن اليوم وهكذا. إيه الحل لمشكلة ال storage دي بقى؟ إزاي نعدل ال algorithm علشان ميحتاجش extra storage؟ الحل بسيط .. إحنا ممكن بدل منبدأ من ال most significant bit إحنا ممكن نبدأ بال least , يعني بدل مبنرتب السنين فالشهور فالأيام , ممكن نرتب الأيام فالشهور فالسنين , بشرط إن إحنا نستخدم stable sorting algorithm , بالطريقة دي مش هنحتاج extra storage , تعالى نشوف الطريقة دي على المثال اللي فات بتاع ال dates :

أول خطوة نرتب بناءا على الأيام بالشكل ده :

تاني خطوة نرتب الناتج بناءا على الشهور بالشكل ده :

تالت خطوة نرتب الناتج بناءا على الأيام بالشكل ده :

هو ده بالظبط ال Radix sort , لإن كلمة radix معناها الأساس أو أساس النظام العددي (زي مثلا النظام العشري الأساس بتاعه 10), وده لإن ال algorithm بيعتمد على الأساس ده اللي هو بيكون ال k بتاع ال counting sort في حالة إننا مستخدمين ال counting sort ك subroutine لل Radix sort , نشوف ال pseudocode بتاع ال Radix بسيط جدا عبارة عن سطرين:

• سطر 1 بي loop حسب عدد ال digits من ال least ل ال most .
• سطر 2 بيستخدم stable sorting algorithm علشان يرتب ال input بناءا على ال digit i .

طبعا لو استخدمنا ال counting sort في السطر 2 ال running time بتاع ال Radix sort هيكون عبارة عن Θ(d(n + k) , بحيث إن ال n + k ده ال running time بتاع ال counting sort وال d هي عدد ال digits لإن ال counting sort بيتنفذ عدد من المرات يساوي عدد ال digits . طبعا ال k بيكون قليل جدا , في النظام العشري الطبيعي مثلا بيساوي 9 , وال d كمان بيكون constant , فكدة ال running time بتاع ال Radix sort بيكون linear أو O(n) .

وده implementation لل Radix sort بلغة ال C :

https://github.com/hossamnasser938/Introduction-to-Algorithms-TextBook/blob/master/radix_sort.c 

Bucket sort

طبعا إحنا عارفين من الفصل التاني إن ال Insertion sort ال running time بتاعه quadratic يعني O(n²) في ال worst case , ولكن ال insertion sort فيه ميزة إنه سريع مع دخل قليل , بمعنى إنك لو هترتب 50 أو 100 عنصر عمليا ال insertion sort بيكون أسرع من ال Merge وال Heap وال Quick , علشان كدة لو عدلت ال Quick أو ال Heap أو ال Merge وخليته يستخدم نفسه لما يكون الدخل كبير ويستخدم ال insertion مع الدخل القليل ال algorithm الناتج هيكون أسرع عمليا , والطريقة دي شفناها في الفصل السابع مع ال Quick sort .

ال Bucket sort بيعتمد إنه يقسم الدخل لمجموعات صغيرة, العناصر اللي جوة كل مجموعة مش مرتبة ولكن المجموعات نفسها من برة مترتبة(يعني كمثال لو الدخل عبارة عن مجموعة عناصر قيم كل عنصر في range من 1 ل 100 فممكن نقسم الدخل ده ل 10 مجموعات المجموعة الأولى فيها العناصر اللي قيمها في ال range من 1 ل 10 والمجموعة التانية فيها العناصر اللي قيمها في ال range من 11 ل 20 وهكذا) , ويرتب كل واحدة لوحدها بال insertion sort وبعدين يضم المجموعات على بعض (concatenation) فيطلع الناتج ال sorted array.

مشكلة ال Bucket sort إنه عليه constraint إنه بيفرض إن الدخل اللي جايله بيخضع لشرطين:

• الدخل عبارة عن أرقام في ال range من 0 ل 1 (يعني أرقام عشرية  floating-point).
• الأرقام دي متوزعة uniformally وده له تعريف رياضي ولكن تسهيلا ده معناه إن الأرقام متوزعة في ال range ده بشكل منتظم (يعني كمثال لو ال input عبارة عن 10 عناصر قيمهم في ال range من 1 ل 100 فلو العناضر متوزعة uniformally نقدر نتوقع بشكل كبير إن عنصر هيكون قيمته في ال range من 1 ل 10 وعنصر هيكون قيمته من 11 ل 20 وعنصر هيكون قيمته من 21 ل 30 وهكذا , متوزعين على ال range بشكل منتظم).

ال Bucket sort من إسمه هيقسم الدخل على مجموعة من ال buckets (كلمة bucket يعني دلو) وبعدبن يرتب كل bucket لوحده وبعدين يعمل concatenation للعناصر اللي في ال buckets فتنتج ال array المترتبة , هو بيستخدم في تمثيل ال bucket برمجيا linked list , ودي data structure هنشوفها بالتفصيل في الباب التالت الفصل العاشر , اللي محتاج تعرفه دلوقتي عن ال linked list إنها data structure أقدر أخزن فيها عناصر وأعمل عمليات عادية زي insertion أو deletion وهكذا.

نشوف ال pseudocode بتاع ال Bucket sort :

• هنا بيعتمد إنه معاه array of buckets أو array of linked lists إسمها B وعدد ال buckets نفس عدد ال input .
• سطر 1 بيخزن عدد عناصر ال input .
• سطر 2 : 3 بيلف على عناصر ال input ويخزن كل عنصر في ال bucket بتاعه أو ال linked list .
• سطر 4 : 5 بيلف على ال buckets يرتبها باستخدام ال insertion sort .
• سطر 6 بيجمع (concatenate) ال buckets مع بعض ويكون ده الناتج النهائي .

هنا بيضرب قيمة العنصر في عدد عناصر الدخل ويحسب ال floor للناتج ويكون ده هو ال index بتاع ال bucket بتاع العنصر الحالي , كمثال لو n = 100 و A[i] = 0.55 فهيخزن ال 0.55 في ال bucket للي ال index بتاعها 55 , لو ال A[i] = 0.33 فهيخزن ال 0.33 في ال bucket اللي ال index بتاعها 33 وبكدة لما يعمل concatenation في سطر 6 ال 0.33 هتيجي قبل ال 0.55 ولو عنصرين جم في نفس ال bucket هيترتبوا باستخدام ال insertion sort في سطر 5 .

الصورة دي بيوضح فيها إزاي ال Bucket sort بيشتغل على دخل مكون من 10 عناصر.

ال expected running time بتاع ال Bucket sort يعتبر linear أو Θ(n) وده ليه إثبات طويل.

وده implementation لل Bucket sort بلغة ال C :

https://github.com/hossamnasser938/Introduction-to-Algorithms-TextBook/blob/master/bucket_sort.c